GCN的入门博客,主要参考了这里。
convolution to graph
CNN在特征提取领域十分强大,而图像本身可以看作是具有非常规则网络结构的图形,每个像素即一个节点。因此我们尝试将convolution推广至任意图。
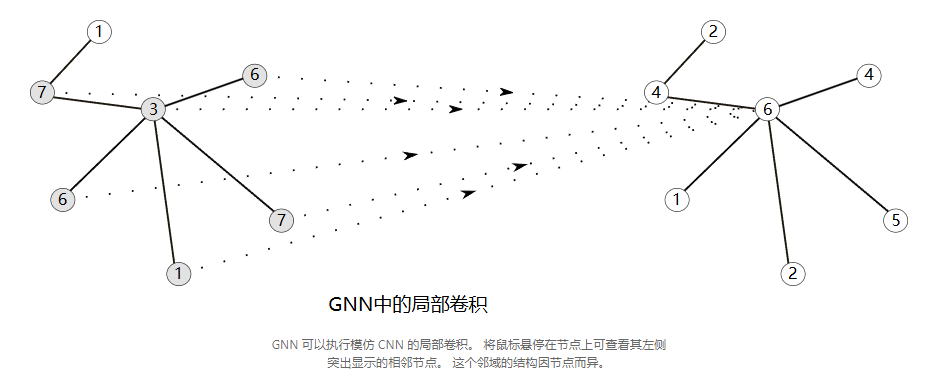
polynomial filters 多项式滤波器
graph laplacian
我们定义图的邻接矩阵A,对角度矩阵D,(Dii的值是第i个节点的邻接边数量)。图的laplacain矩阵定义为 L = D - A。如下是一个示例。
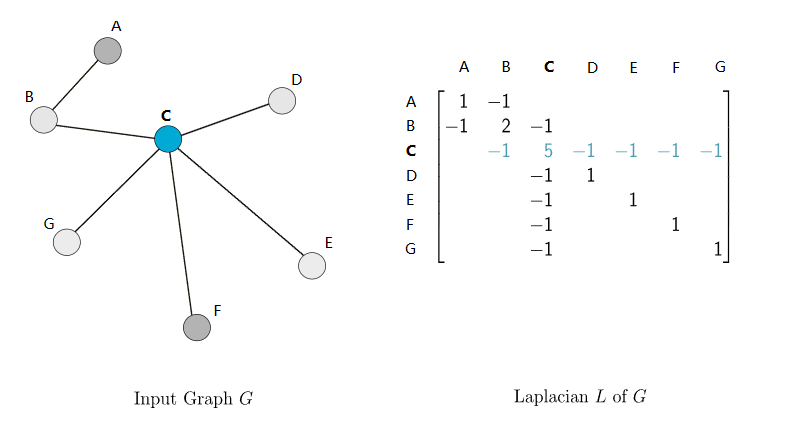
可见,laplacain矩阵仅依赖于图的拓扑结构,而与节点特征无关。
Polynomials of the Laplacian
构造如下的laplacian多项式
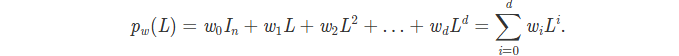
L即laplacian矩阵,其幂次矩阵与本身形状相同。如上的多项式可以通过一个向量 **w **表示,其每个维度的值对应每一项的系数。
这些多项式可被视作“滤波器”,而 w 是滤波器的权重。
将每个结点的特征向量组合为节点特征矩阵 x ,定义其于滤波器的卷积
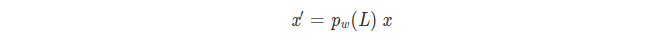
若w0=1,wi=0,x‘=x。
若w1=1,wi=0,x’=Lx,可见,每个结点的特征与其直接邻居特征相结合。
L矩阵有着如下的规律
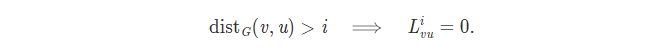
即如果将 x 与次数为d的多项式进行卷积,
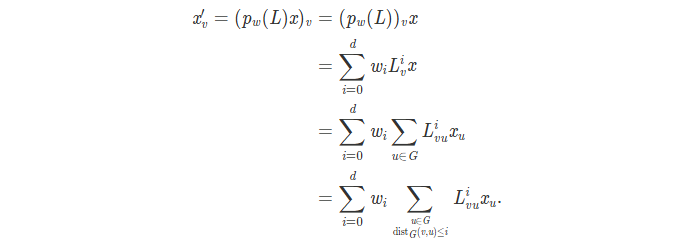
即节点的卷积实际上只与不超过d步距离的节点关联,可见滤波器是局部的,局部的程度完全由d决定。
chebNet
chebNet对polynomial filters 进行了改进,其多项式形式如下
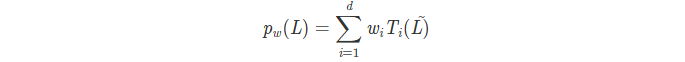
其中,Ti 是第 i 阶的第一类切比雪夫多项式,而 L~ 是使用 L 的最大特征值定义的归一化拉普拉斯算子:
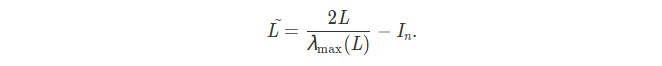
why 设计like this?
- L是半正定的——其所有特征值都不小于0。如果L的最大特征值大于1,其多次幂矩阵的项会很大。 L~ 相当于做了放缩,其特征值绝对值都小于1。从而也可以在选择高阶系数在相同的颜色尺度上显示结果 x‘。
- 切比雪夫多项式使得插值更具数值稳定性。(可以参考这里: Chebyshev Polynomials )
节点定价性
可以证明多项式滤波器的输出与节点顺序改变无关。即其是节点序列等变的。
embedding computation
现将如 chebNet 的多项式与非线性层堆叠来构建 GNN ,假设有k个不同的 filter 层,他们有着各自的权重 w_k。计算如下。

可见,在不同节点的滤波器权重是相同的,这和CNN是相似的。
现代GNN
在之前提到的 polynomial kernel 中,
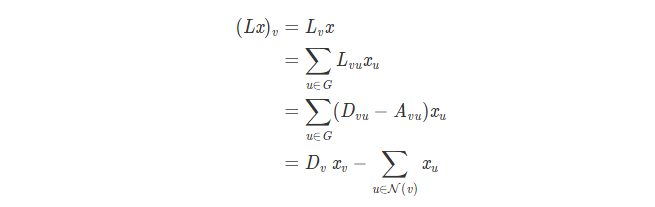
其结果可以看作是两个步骤产生的:与节点本身特征结合 + aggregate 邻居节点的特征。
考虑不同的结合 和 聚合步骤?
1 | 同时要保证convolution是节点顺序等变的,这可以保证aggregate是节点顺序等变的来实现。 |
convolution 可以看作是 message passing ,重复进行1-hop的convolution k次,可以接收到k-hop内的所有节点信息。
message passing 是很多GNN架构的核心。
GCN
Semi-Supervised Classification with Graph Convolutional Networks
GAT
Graph Attention Networks
GraphSAGE
Inductive Representation Learning on Large Graphs
GIN
How Powerful are Graph Neural Networks?
博客还提供了网络可视化,可以自由调整图拓扑结构与参数,参考这里。
Convolution:Local to Global
之前所介绍的方法都只局限在局部卷积,虽然特征能通过执行多次卷积来传递到更远的地方,但是接下来会介绍一种global convolution(全局卷积)。Spectral Networks and Locally Connected Networks on Graphs
spectral convolutions光谱卷积
1 | 提前说明,节点的特征向量(feature vector)指能够表示节点特征的嵌入向量,与矩阵特征值对应的特征向量(eigenvectors)有异。之后的叙述不会严格区分二者的中文表达。 |
以标量为例,假设每个节点的特征表示为 xi ,所有节点的特征向量组合为特征向量 X (常规情况下是矩阵,只不过这里只考虑一维的节点特征),并将其规范化(使向量的各维度值平方和为1)。定义
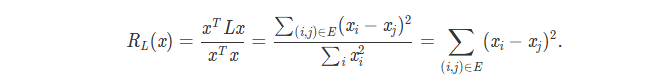
可见,对于邻接节点分配较小特征表示的特征向量会使得Lx值较小。
L是一个实对称阵,即其有n个实数特征值,并且特征值对应的特征向量可以正交归一化(组成正交单位阵)。
可以证明的是,随着特征值增加,其对应的特征向量变得不平滑。平滑,指向量中的纬度值变化较小。

将这组L的特征值称为 spectral (谱)。将L的光谱分解表示为。(实对称阵的相似对角化)
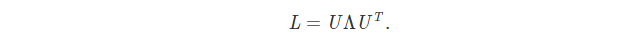
其中 Λ 是特征值按从小到大顺序依次从上到下排列在对角线上组成的对角矩阵,U 是对应顺序的特征(列)向量组成的特征向量矩阵。如下,其中 𝜆1≤…≤𝜆𝑛。

特征向量 ui 组成的 U 即单位正交阵,满足 U^T U = I 。同时 ui 也是 n 维向量空间的一组基,可以通过其线性组合表达空间中任意向量 x 。
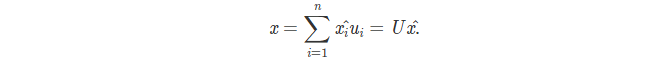
其中 x^ 是系数组成的向量,称为节点特征向量 x 的光谱表示。由 U 的性质可知

上式提供了 n 维空间的任意向量自然表示和光谱表示的转换方法。
Spectral Representations of Natural Images
小孩都知道,图像也是一种特殊的图结构,每个像素组成一个节点,其邻居节点的个数(3,5,8)因中心节点的位置而异。如果图像是灰度图,节点的值是一个表示像素黑暗程度的实数。如果是彩色,每个值将是一个3维向量,即(RGB)通道值。
对图像的每个通道做如下实验:
将某通道所有像素值组成 feature vector x 。
获得其频谱表示 x^
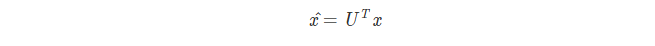
截断到前m各分量,即把后 n - m 个分量置零。这等效于仅使用前 m 个 eigenvectors 进行计算
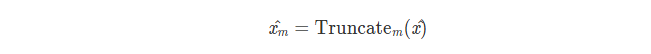
转回其自然向量
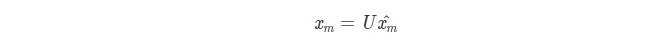
使用 xm 重建图像。博客提供了一个图像随m变化的可视化呈现,点击这里。
可以得出的结论是:对于任何图像 x ,我们可以认为光谱表示 x^ 的初始项捕捉到了全局范围内的趋势,即低频成分,而后来的相泽捕捉到了局部上的细节,即高频成分。
embedding computation
假设网络有k层,每一层都有可学系的参数w,即滤波器权重,这些权重与节点特征的谱表示进行卷积,由之前的讨论可知,权重数量要等于计算谱表示的特征向量数量。此外,由于拉普拉斯特征向量在图上的平滑性,使用谱表示自动为相邻节点获取相似表示强加了归纳偏置。(?)
仍假设节点特征是一维的,每层的输出都是节点表示的向量作为行组成的矩阵 h(k)。

为节点定义顺序,从而得到 L 矩阵,计算其特征向量矩阵 Um 。embedding computation计算如下。

再谈spectral convolution
与 laplacian filter 类似,spectral convolution也可以被证明是节点顺序等变的,即不同节点顺序的输入会得到相同的结果。
spectral convolution仍有一些缺陷
- 对于大图,从 L 计算 Um 矩阵是很困难的
- Um 计算矩阵乘法复杂度很大
- 所学习到的 filter 是局限于输入图的,其不能很好的转移到结构显著不同的新图
Global Propagation
一种更简单的方法大是通过pooling 节点的 embedding,再使用graph embedding 来更新节点 embedding。然而这种方法往往忽略了spectral convolution能捕捉的图的基础拓扑结构。
GNN parameters
之前所有的embedding计算都是可微的,既可以像标准神经网络一样,定义损失,进行端到端的训练。
node classification
常见的节点分类损失函数设计如下
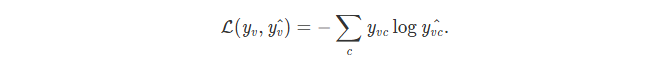
y^v,c 是节点 v 属于类别 c 的预测概率。
如果是半监督,只有部分节点有标签,定义损失
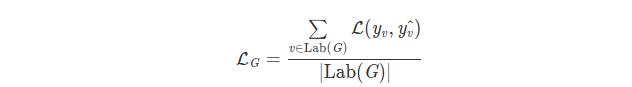
我们只对 label 节点(labG)计算损失。
graph classification
通过聚合节点表示可以得到图表示,该表示可被用于任何图级别的任务。(不局限于分类)
link prediction
sampling 相邻/不相邻节点,再使用向量对来预测边的存在与否。损失函数设计如下
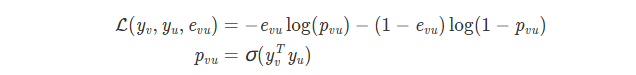
其中 e_{vu} = 1当且仅当节点 v 和 u 之间有边,否则为0。
node clustering
节点聚类——通过学习到的节点表示实现。
预训练图。
自监督方法:强制相邻节点获得相似的嵌入。
终
两篇综述推荐
A Comprehensive Survey on Graph Neural Networks
Graph Neural Networks: A Review of Methods and Applications
dropout
图中的dropout可直接应用于参数,比如将矩阵的一行置零。
也有一些特定的技术,随即移除图中的整个边。如DropEdge(DropEdge: Towards Deep Graph Convolutional Networks on Node Classification)
other graph
上述的讨论局限于无向图,然而实际上空间卷积的变体可以用于有向图,时序图,异构图等结构。
pooling
将节点特征aggregate成图特征需要pooling技术,即
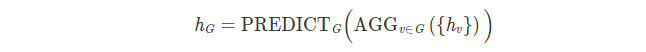
一些技术:
sortpool
diffpool
sagpool
