概述
鱼书三件套第一本的读书笔记，相关电子版书籍请见。
1 | 本书面向深度学习0基础人群，逐一介绍深度学习涉及的基础知识。需要具备一定线性代数，高等数学，python基础。 |
（持续更新中）
Python入门
略
感知机
感知机接受输入信号，获得输出信号。信号只有0、1两个值，代表流，和不流。输入通过某种运算得到结果，结果大于0，输出为1，反之则输出0。以下是一个例子
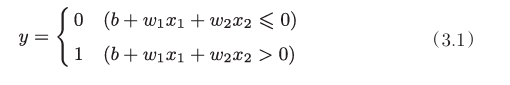
x为输入，w为权重，b为偏置，y为输出。图示如下，偏重也通过权重的方式展示。
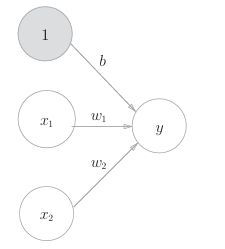
我们很容易地联想到门电路也可以用感知机表示，而门电路可以组成更复杂的运算。这表明（多层）感知机在理论上可以表示计算机。
神经网络
感知机和神经网络？
感知机中，为了使其能够有合理的表示，需要人为设定参数，而神经网络可以从自动的从数据中“学习”这些参数。
神经网络的结构简化版如下，输入层也称为第0层，从左向右依次增加。可见，结构与感知机很类似。
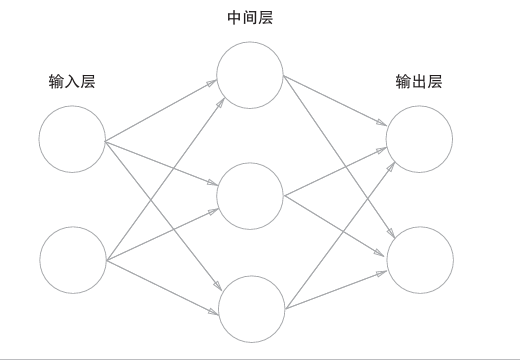
1 | 上图是一个实例。特别的，网络中所有神经元都存在箭头的链接时称为全连接网络 |
我们将（3.1）转化为更简洁的形式，使用函数将其封装。
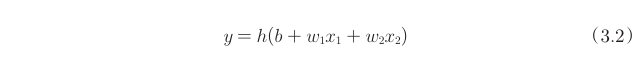
其中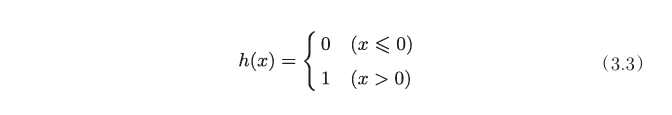
就是所说的激活函数，即决定如何激活输入的信号总和。
激活函数
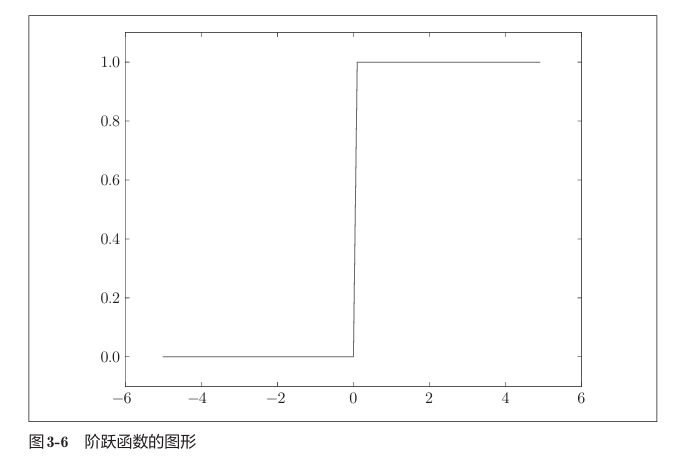
在感知机中，激活函数采用了阶跃函数，如下图，然而神经网络的选择另有其人。
sigmoid
函数如下
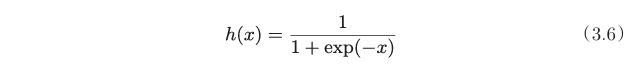
我们在坐标上展示
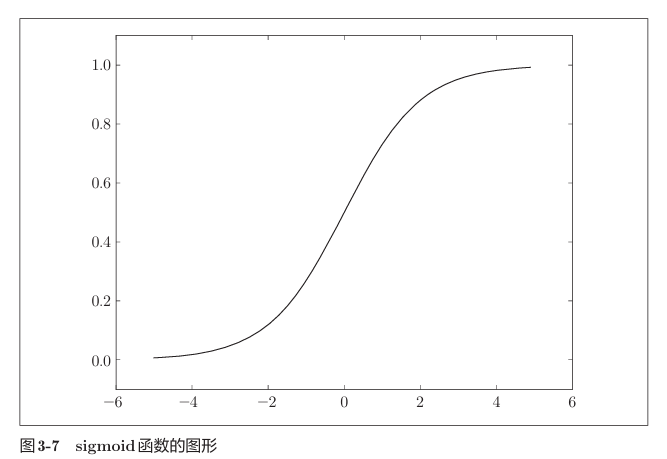
可以看到sigmoid函数是一条平滑的曲线，神经网络中流动的也不是单纯的0/1值，而是连续的实数信号。
与阶跃函数相同，它也是非线性函数，也在输入较小时返回0，输入较大时返回1。
1 | 神经网络的激活函数一定要使用“非线性函数”，如果采用了线性函数，问题在于：无论怎样增加网络的层数，总是存在一个等效的单层网络，无法发挥叠加层带来的优势。 |
ReLU
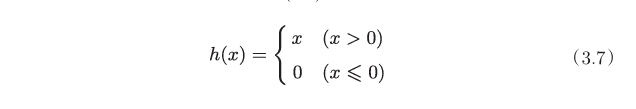
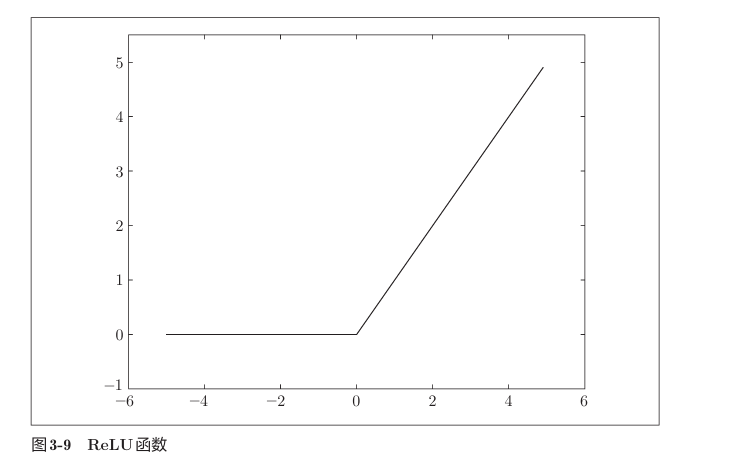
输出层
输出层的激活函数与隐藏层不同，如果神经网络对应回归问题，则使用恒等函数。如果是分类问题，则使用softmax函数。
1 | 机器学习的问题大致可以分为分类问题和回归问题。分类问题是数据属于哪一个类别的问题。比如，区分图像中的人是男性还是女性的问题就是分类问题。而回归问题是根据某个输入预测一个（连续的）数值的问题。比如，根据一个人的图像预测这个人的体重的问题就是回归问题（类似“57.4kg”这样的预测）。 |
softmax函数可以用下面的式（3.10）表示。
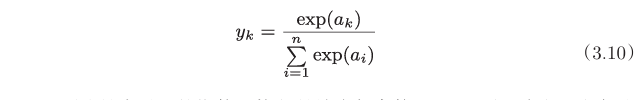
如果输出层有n个神经元，第k个神经元输出为$y_k$，输入为$a_k$
softmax函数的输出是0.0到1.0之间的实数。并且，softmax 函数的输出值的总和是1。因为有了这个性质，我们才可以把softmax函数的输出解释为“概率”。因此，神经网络在进行分类时，输出层的个数即为类别个数，把输出值最大的神经元所对应的类别作为识别结果。并且，即便使用softmax函数，输出值最大的神经元的位置也不会变，因此输出层的softmax函数可以省略。
神经网络的学习
学习，指从训练数据中获得最优参数的过程，
训练数据和测试数据
机器学习中，一般将数据分为训练数据和测试数据两部分来进行学习和 实验等。首先，使用训练数据进行学习，寻找最优的参数；然后，使用测试数据评价训练得到的模型的实际能力。
1 | 为什么需要将数据分为训练数据和测试数据呢？因为我们追求的是模型的泛化能力。 |
泛化能力是指处理未被观察过的数据（不包含在训练数据中的数据）的能力。获得泛化能力是机器学习的最终目标。
损失函数
神经网络以某个指标为线索寻找最优权重参数。神经网络的学习中所用的指标称为损失函数（loss function）。损失函数是表示神经网络性能的“恶劣程度”的指标，即当前的神经网络对监督数据在多大程度上不拟合，在多大程度上不一致。
均方误差
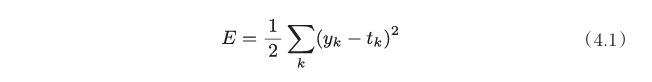
yk是表示神经网络的输出，tk表示监督数据，k表示数据的维数。
监督数据可以采用onehot编码的形式表示，正确解为1，反之为0。
交叉熵误差
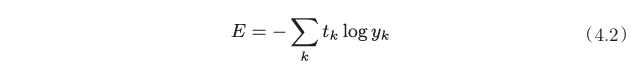
yk是神经网络的输出，tk是 正确解向量。仍采用onehot编码的形式表示。
例如数据做10个标签的分类任务，正确解为第三个标签。则向量表示如下。
1 | 在计算log时，可以加上一个微小值delta。这是因为，yk会==0，添加一个微小值可以防止负无限大的发生。 |
mini-batch
如果要求所有训练数据的损失函数的总和，以交叉熵误差为例，可以写成下面
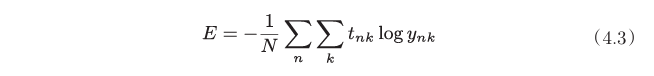
这里,假设数据有N个，tnk表示第n个数据的第k个元素的值（ynk是神 经网络的输出，tnk是监督数据）。
如果以全部数据为对象求损失函数的和，则计算过程需要花费较长的时间。因此，我们从全部数据中选出一部分，作为全部数据的“近似”。称为mini-batch。
数值微分
梯度下降
神经网络需要在学习时找到最优参数（权重和偏置），即，使损失函数最小，我们借助梯度来计算。即，函数的取值从当前位置沿着梯度方向前进一定距离，然后在新的地方重新求梯度，再沿着新梯度方向前进， 如此反复，不断地沿梯度方向前进。这就是梯度下降法。而梯度使用定义计算，即，变量变动微小的值 分之 对应函数的变化值。
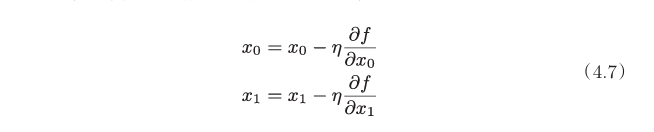
式（4.7）的 η表示更新量，在神经网络的学习中，称为学习率（learning rate）。学习率决定在一次学习中，应该学习多少，以及在多大程度上更新参数。
1 | 学习率过大的话，会发散成一个很大的值；反过来，学习率过小的话，基本上没怎么更新就结束了。也就是说，设定合适的学习率是一个很重要的问题。 |
像学习率这样的参数称为超参数。这是一种和神经网络的参数（权重和偏置）性质不同的参数。相对于神经网络的权重参数是通过训练 数据和学习算法自动获得的，学习率这样的超参数则是人工设定的。 一般来说，超参数需要尝试多个值，以便找到一种可以使学习顺利进行的设定。
SGD
如果mini-batch随机选择数据，则称随机梯度下降法（SGD）
总结
神经网络的学习过程，就是
- 从总体训练集挑选batch的数据，计算loss，并调参；
- 重复上步直至所有数据都被选择，该过程称为一个epoch。
- 训练多个epoch，直至acc收敛。
误差反向传播法
数值微分法及其耗时，本节介绍一个高效梯度计算方法。
计算图
计算图将一个数学过程简化为图示，例子如下。
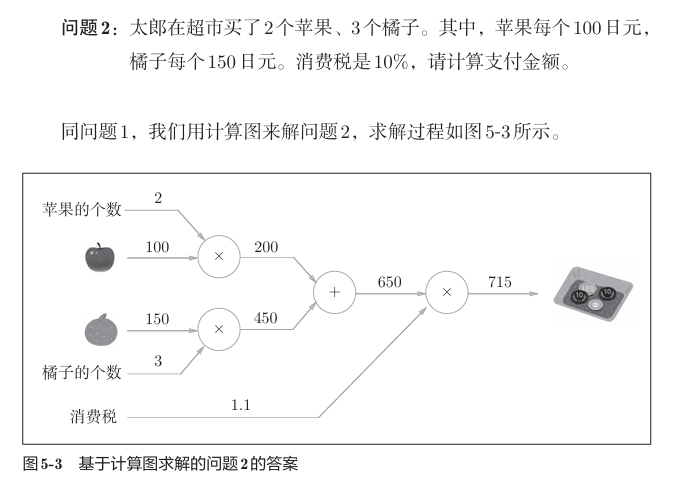
我们求解金额时，要进行从左到右的计算，（如上2乘100，3乘150，再相加，再乘1.1)，其称为正向传播。相应的也有反向传播，即我们接下来介绍梯度求解的基础。
神经网络类比到买水果，参数就相当于水果的价格，个数，消费税。
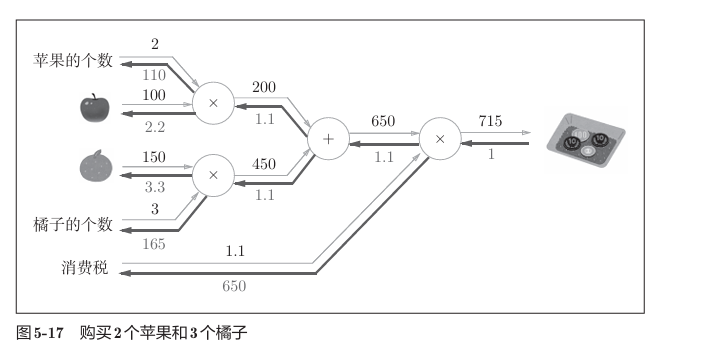
如上，由链式法则，我们将每个结点的导数传递，如黑色加粗所示。可以看到加法节点和乘法节点在传递时有着各自的规律。
激活函数
相比于买水果，神经网络有着更复杂的激活函数，我们也同样求其反向传播。
ReLU
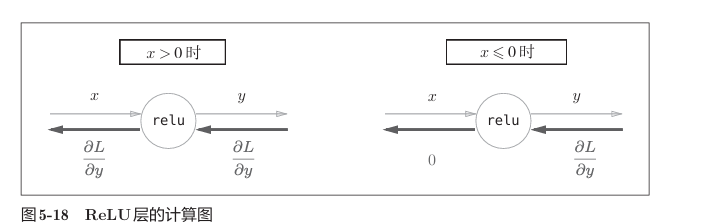
sigmoid
易得
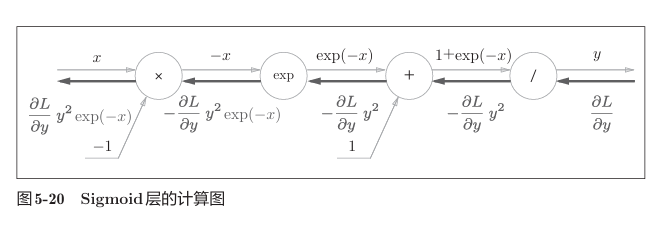
简化为
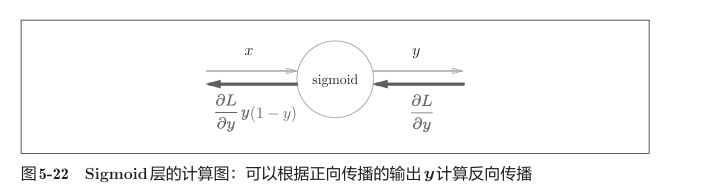
Affine层
神经网络的正向传播可以通过矩阵乘法来实现。我们把这种计算称为放射（affine）。
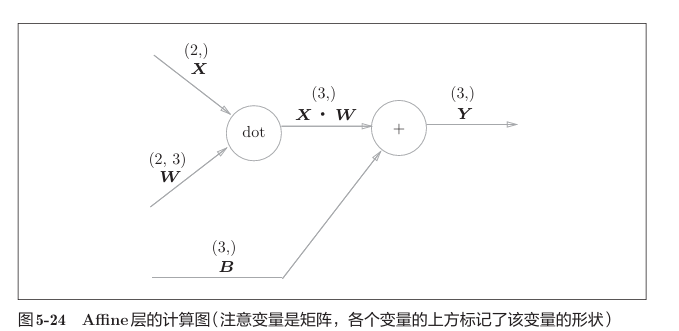
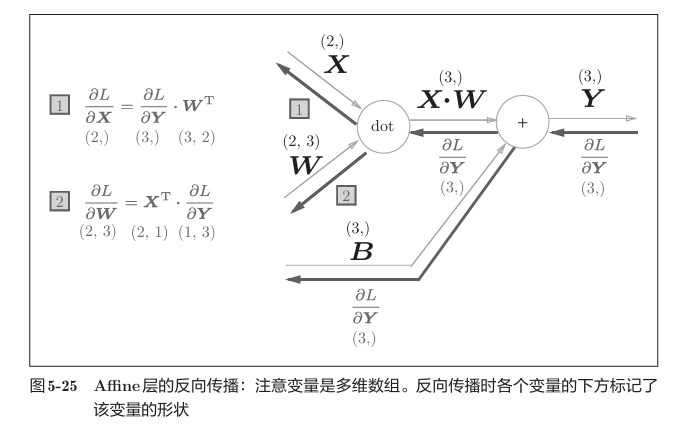
相比于之前的计算图，将标量更换为了矩阵，对应的反向传播如下。
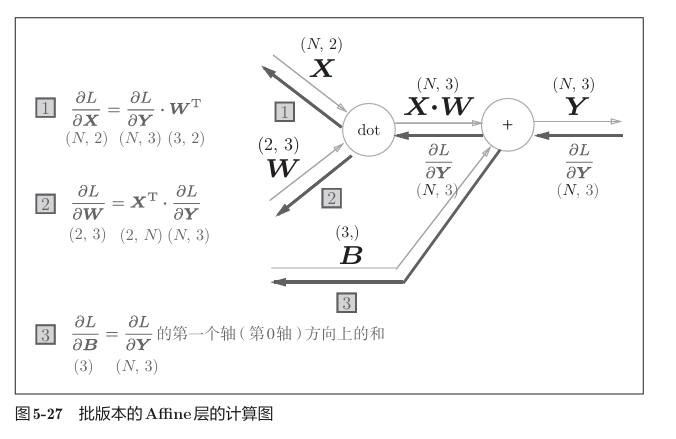
批处理版本
softmax&loss层
计算图如下
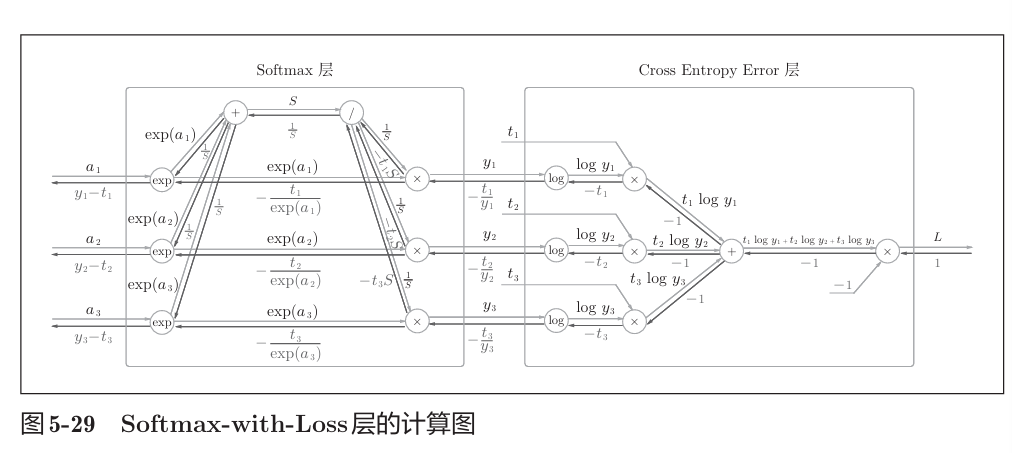
loss采用了交叉熵损失，这是一个三分类的例子。
简化为
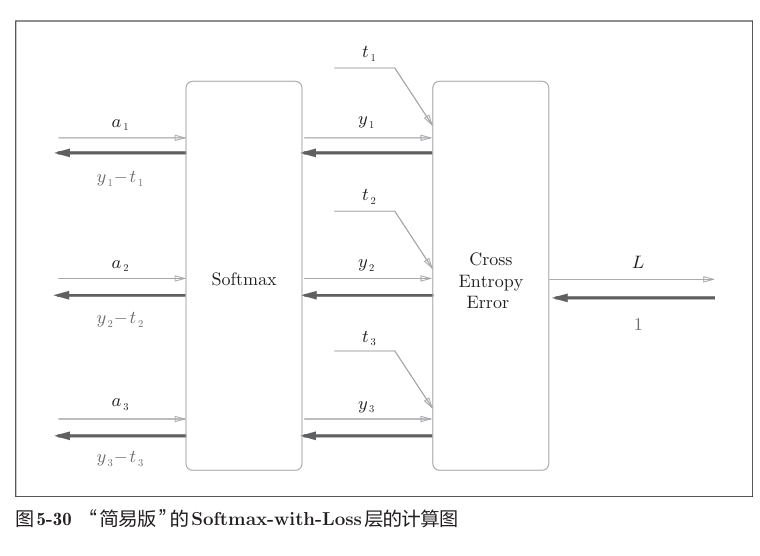
可见softmax的反向传播数字异常的美观而直接——即输出与监督数据的差值。
1 | 实际上，是为了获得美丽的结果而进行了相应的损失函数设计。 |
总结
我们只需要在之前学习的流程中采用误差反向传播法代替微分法求梯度，就可以得到一个更优质的神经网络。值得一提的是，我们今后都会使用前者计算梯度，而后者的作用在于可以检查前者的正确性，即梯度确认。
学习的技巧
参数更新
神经网络的学习的目的是找到使损失函数的值尽可能小的参数，即最优参数解决这个问题的过程称为最优化。
我们曾介绍了SGD方法，但是其有着一定的缺点。
例如对于函数
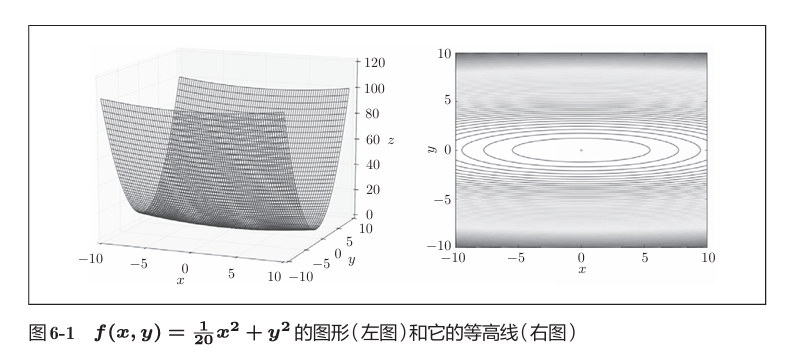
其梯度
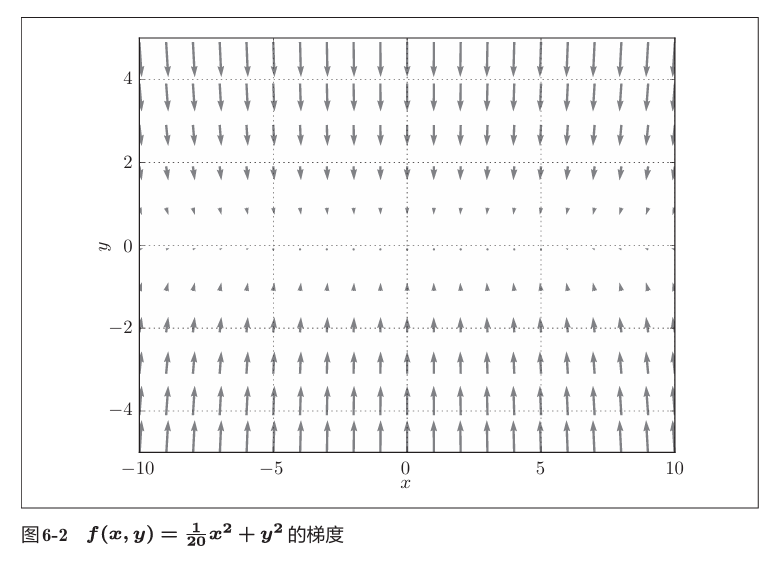
会发现，梯度并非指向最小值的方向。最小值在（0，0）取得，但是很多点的梯度并非指向该点。
在此情况下，使用SGD会使得路径呈“之”字形。
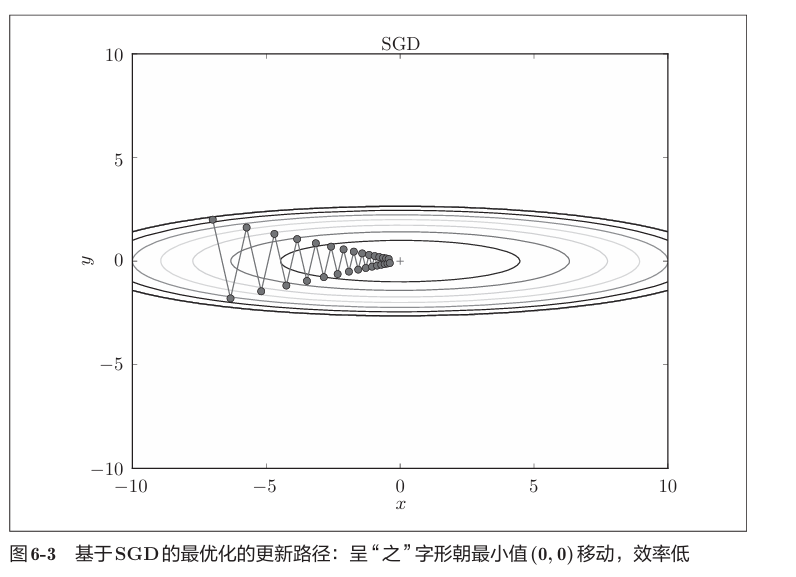
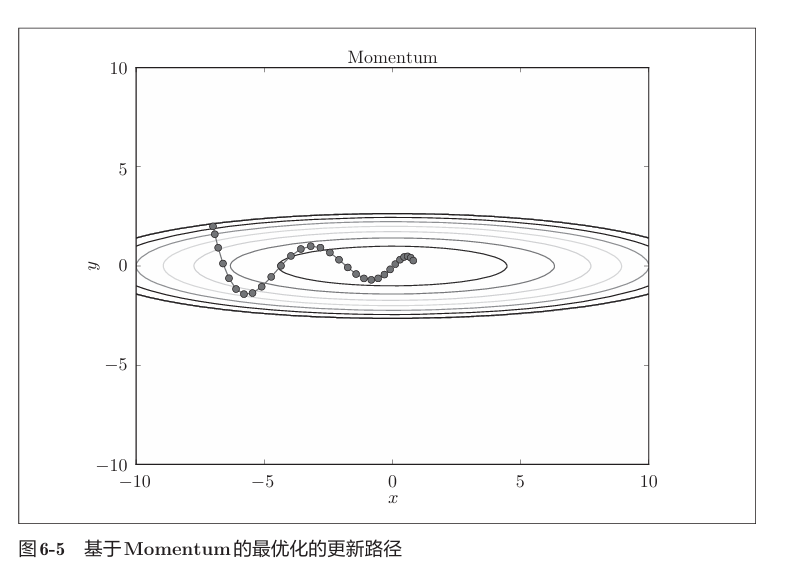
Momentum
使用Momentum，我们发现 “之”字形的“程度”减轻了。这是因为虽然x轴方向上受到的力非常小（梯度很小），但是一直在同一方向上受力，所以朝同一个方向会有一定的加速。反过来，虽 然y轴方向上受到的力很大，但是因为交互地受到正方向和反方向的力，它 们会互相抵消，所以y轴方向上的速度不稳定。
AdaGrad
神经网络学习中，学习率过小， 会导致学习花费过多时间；学习率过大，会导致学习发散。在关于学习率的有效技巧中，有一种被称为学习率衰减（learning rate decay）的方法，即随着学习的进行，使学习率逐渐减小。0
1 | 实际上，一开始“多” 学，然后逐渐“少”学的方法，在神经网络的学习中经常被使用。 |
AdaGrad会为参数的每个元素适当地调整学习率，与此同时进行学习。
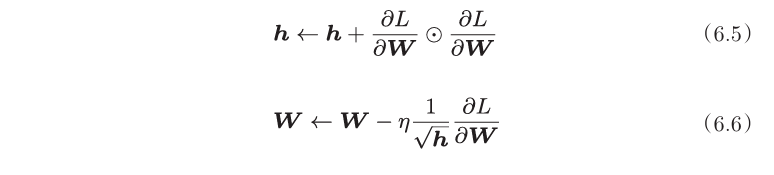
h保存了以前的所有梯度值的平方和，从而调整学习的尺度。即， 可以按参数进行学习率衰减，使变动大的参数的学习率逐渐减小。
使用AdaGrad如下。
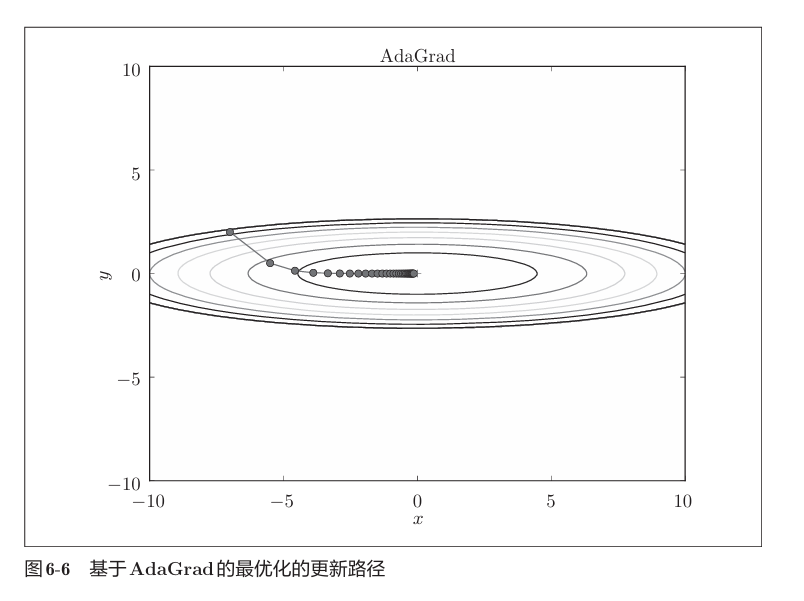
可见，函数的取值高效地向着最小值移动。y方向上的梯度较大，因此刚开始变动较大，但是后面会根据这个较大的变动按比例进行调整，减小更新的步伐。因此，y轴方向上的更新程度被减弱，“之” 字形的变动程度有所衰减。
Adam
Adam结合了上述两者。
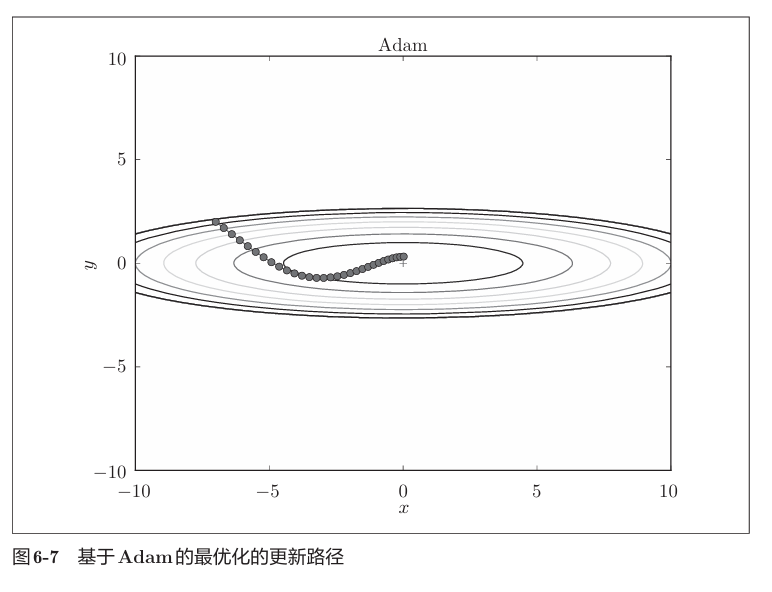
1 | （目前）并不存在能在所有问题中都表现良好的方法。这4种方法各有各的特点，都有各自擅长解决的问题和不擅长解决 的问题。一般而言，与SGD相比，其他3种方法可以学习得更快，有时最终的识别精度也更高。 |
权重的初始值
sigmoid的初始值——Xavier
权重的初始值应该如何设置？
我们不妨先假设参数分布满足均值为0，标准差为1的正态分布。
一共生成1000个数据，通过5层每层100的神经元的网络，使用sigmoid函数。每层的激活值如下。
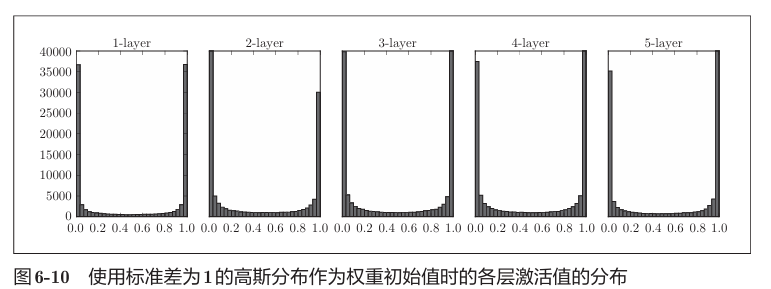
我们发现各层激活值偏向0/1，由sigmoid函数的特点，其导数会趋于0，这样在反向传播中其梯度会逐渐减小，直至消失。即梯度消失。
再假设参数分布满足均值为0，标准差为0.01的正态分布。
我们采用Xavier初始值。即，如果前一层的节点数为n，则初始值使用标准差为1/sqrt(n) 的分布。
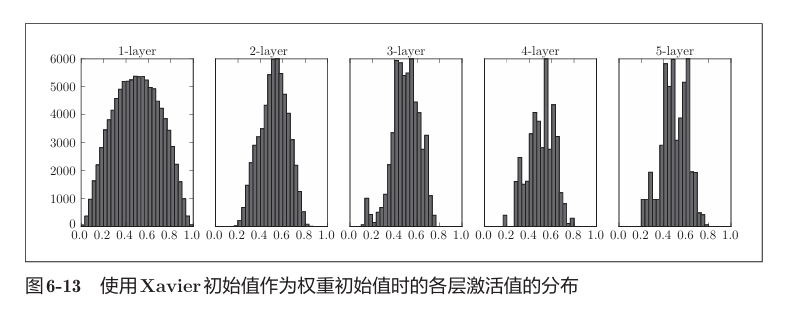
ReLU的初始值——He
当前一层的节点数为n时，He初始值使用标准差为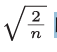
的高斯分布。
Batch Normalization
Batch Norm的思路是调整各层的激活值分布使其拥有适当的广度。为此，向神经网络中插入对数据分布进行正规化的层，即Batch Normalization层。如下
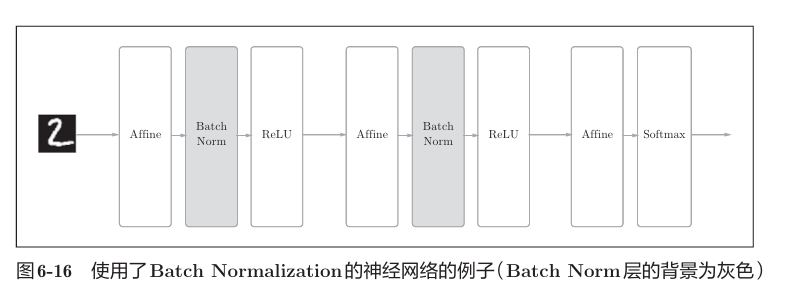
其将每一层的输出归一化（均值和方差一致），消除了X带来的放大缩小的影响，进而解决梯度消失和爆炸的问题
其反向传播
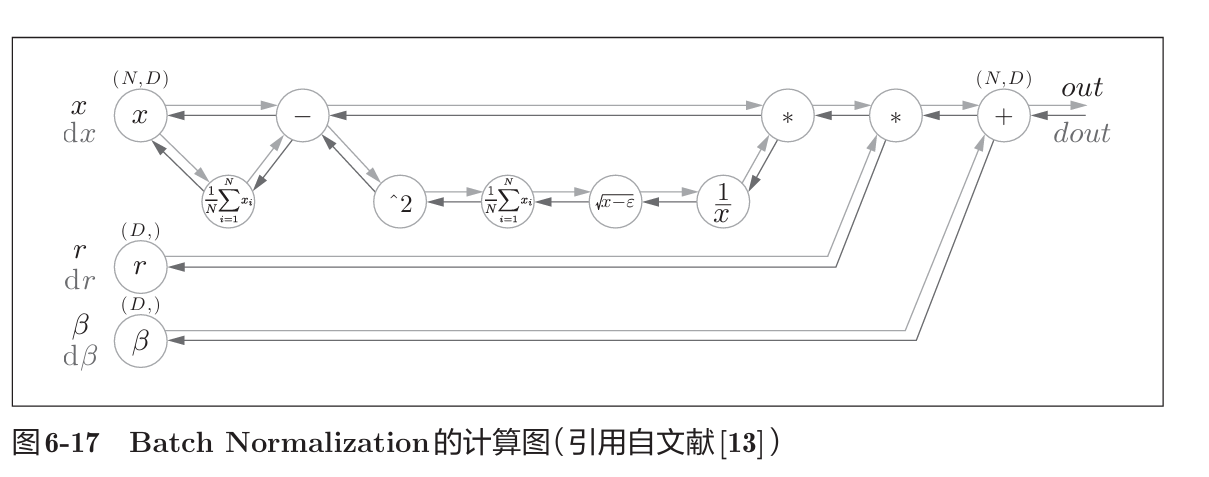
BN的反向传播推到有些复杂，这里仅给出了计算图的示例。
正则化
过拟合指的是只能拟 合训练数据，但不能很好地拟合不包含在训练数据中的其他数据的状态。
发生过拟合的原因，主要有两个。模型拥有大量参数、表现力强；训练数据少。
权值衰减
其通过在学习的过程中对大的权重进行惩罚，来抑制过拟合。具体来说，如果将权重记为W，将其L2范数$\frac{1}{2} \lambda W^2$加到损失函数上，这里$\lambda$是控制正则化强度的超参数。
dropout
Dropout是一种在学习的过程中随机删除神经元的方法。训练时，随机选出隐藏层的神经元，然后将其删除，其不再进行信号的传递。
超参数的验证
验证数据
测试数据用于评估泛化能力，不能评估超参数的性能。因为如果使用测试数据调整超参数，超参数的值会对测试数据发生过拟合。 因此，用于调整超参数的数据，一般称为验证数据。
超参优化
先大致设定一个范围(指像0.001到 1000这样，以“ 10的阶乘”的尺度指定范围)，从这个范围中随机选出一个超参数进行识别精度的评估；根据这个结果缩小超参数的范围。重复这一操作，就可以逐渐确定超参数的合适范围。
1 | 上述方法看起来像大力出奇迹，而贝叶斯最优化能够更“数学”的进行最优化。更多内容可以参考这篇文献，https://arxiv.org/abs/1206.2944。 |
计算的高速化
位精度
我们借助Numpy计算神经网络，其浮点数默认是64位，然而32位也可以无损的（几乎）表达神经网络，并且还有一半的内存占用。
1 | 其实16位的浮点数也不会造成多大的损失，并且更快。但是因为普遍CPU，GPU都是按照32位设计的，并不会带来优化。也就是说要使用神经网络的专用GPU，例如谷歌TPU，其能支持8位的浮点运算。 |
GPU
GPU相比于CPU更擅长计算简单巨量的计算，很适合进行神经网络的计算。我们可以使用Cupy库来平替Numpy，使网络可以在GPU上并行计算。
1 | GPU指Graphics Processing Unit。高端显卡主流有AMD的A卡，和NVIDIA的N卡。NVIDIA有相应的AI加速型号，诸如A100，A800，价格昂贵。 |
卷积神经网络CNN
本章将主要介绍CNN的架构，并利用其进行目标检测任务。
整体结构
之前介绍的全连接层使用Affine层实现，并且后接激活函数层，最后通过softmax层预测概率。下图是一个五层的全连接网络实例。
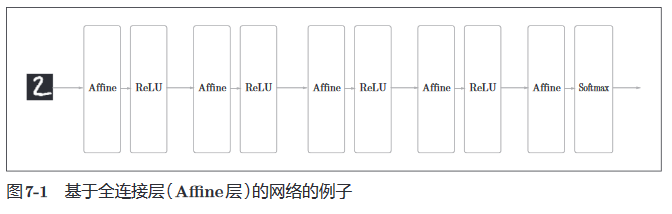
二本章中即将介绍的CNN新加了convolution（卷积）层和pooling（池化）层，取代了部分Affine-Relu的结构，如下所示。
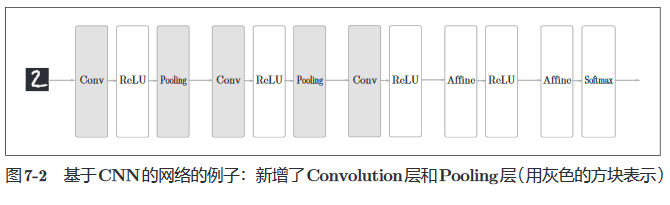
卷积层
卷积层的输入称为输入特征图，输出成为输出特征图。层中对图进行的处理就是卷积运算（也叫滤波器运算）。如下是一个例子。
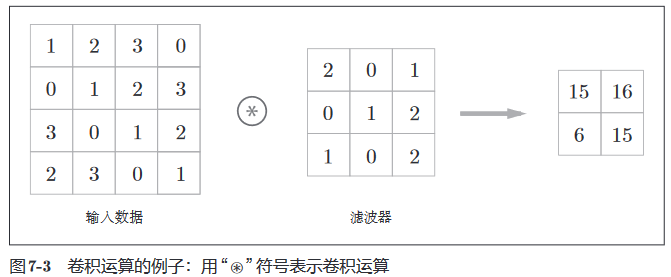
在本例中，输入大小是 (4, 4)，滤波器大小是 (3, 3)，输出大小是 (2, 2)。
1 | 也有的文献中也会用“核” 这个词来表示这里所说的“滤波器”。 |
具体来说，对于输入数据，卷积运算以一定间隔滑动滤波器的窗口并应用。这里所说的窗口是指图 7-4 中灰色的 3 × 3 的部分。如下图所示，将各个位置上滤波器的元素和输入的对应元素相乘，然后再求和（有时将这个计算称为乘积累加运算）。然后，将这个结果保存到输出的对应位置。将这个过程在所有位置都进行一遍，就可以得到卷积运算的输出。
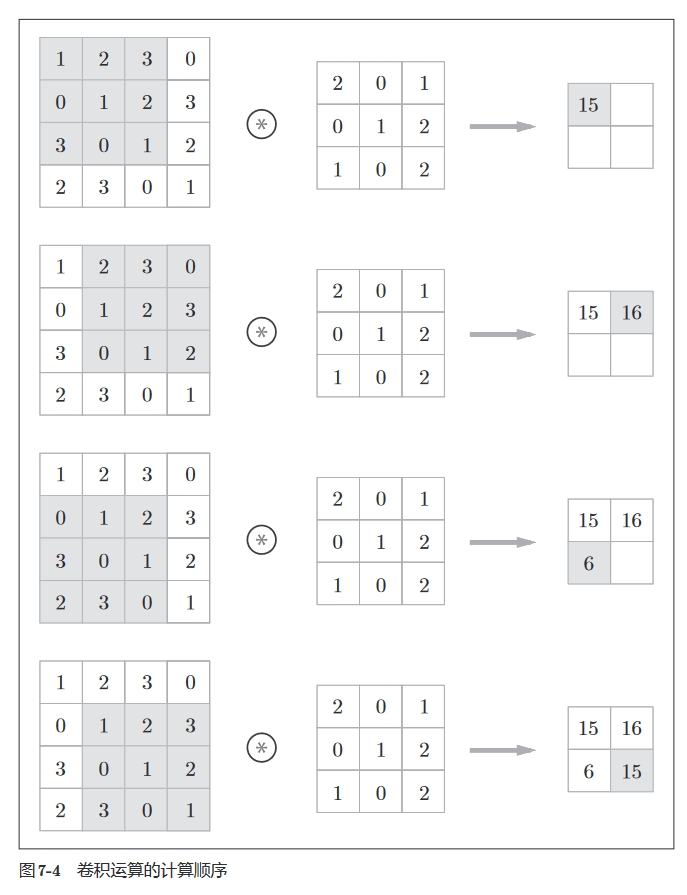
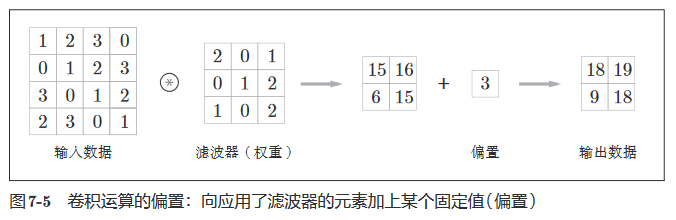
类似的，CNN中也会有偏置的概念，如下。
填充
在进行卷积层的处理之前，有时要向输入数据的周围填入固定的数据（比如 0 等），这称为填充（padding），是卷积运算中经常会用到的处理。比如对大小为 (4, 4) 的输入数据应用了幅度为 1（像素） 的填充，如下所示。
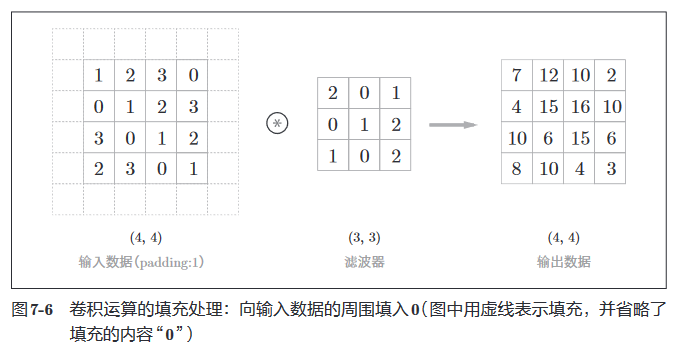
通过填充，大小为 (4, 4) 的输入数据变成了 (6, 6) 的形状。 然后，应用大小为 (3, 3) 的滤波器，生成了大小为 (4, 4) 的输出数据。这个例 子中将填充设成了 1，不过填充的值也可以设置成 2、3 等任意的整数。
1 | 可见，填充的目的是为了避免输入经过多次卷积后输出大小变为1的情况，使得卷积能在保持输入输出大小不变的情况下将数据传给下一层。 |
步幅
应用滤波器的位置间隔称为步幅（stride）。之前的例子中步幅都是 1，如果将步幅设为 2，则如下所示，应用滤波器的窗口的间隔变为 2 个元素。
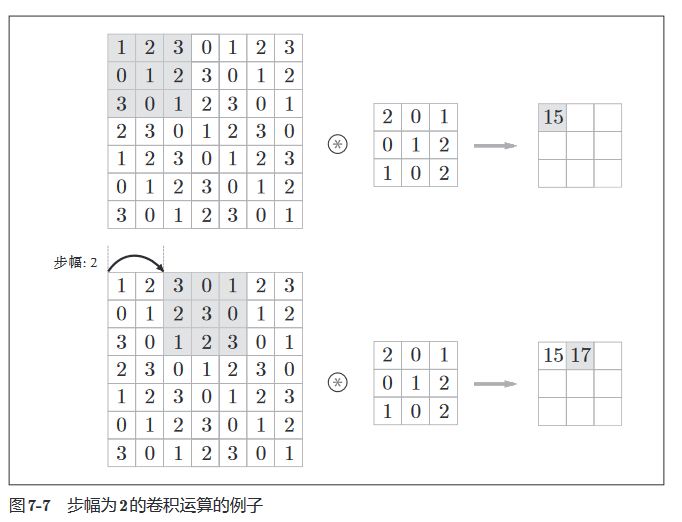
假设输入大小为 (H, W)，滤波器大小为 (FH, FW)，输出大小为 (OH, OW)，填充为 P，步幅为 S。则有。
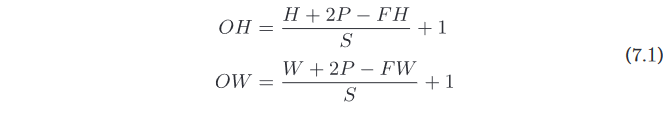
对于图像输入，输入数据是三维数组，其进行卷积运算的示例如下。
可见通过滤波器的输出特征图增加了，我们将结果相加得到输出。
我们采用更直观的图形来展示三维数据的卷积运算。
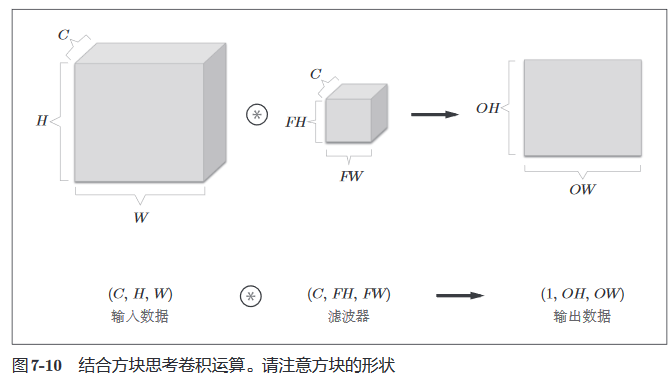
FN、C、FH、FW 分别是Filter Number（滤波器数量）、Channel、Filter Height、Filter Width 的缩写。
我们也可以使用多个滤波器得到通道方向上的多个特征图。
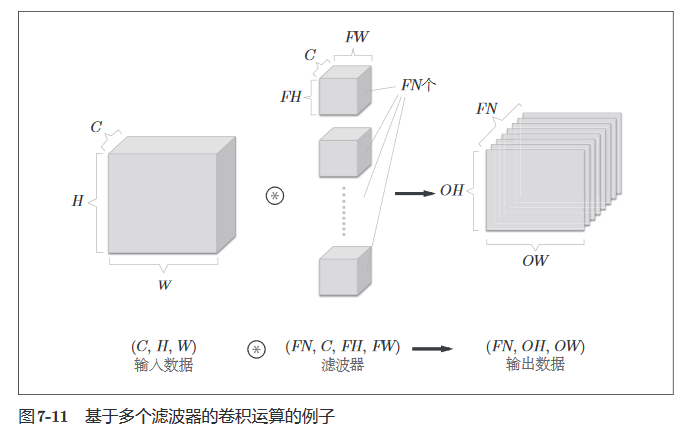
在上图中，我们使用了FN个滤波器，从而输出了FN个特征图。
再引入偏置。每个通道有一个偏置。
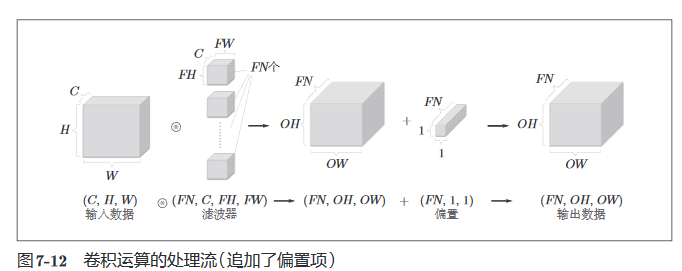
再引入mini - batch，对N个数据进行计算。
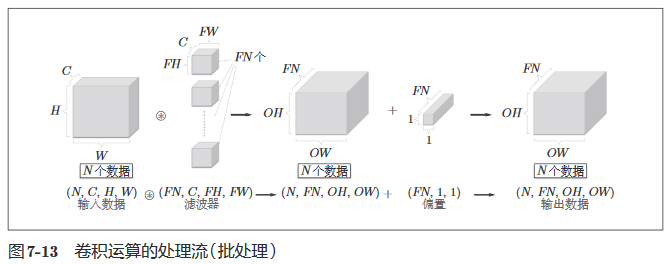
池化层
池化是缩小高、长方向上的空间的运算。如下所示，进行将 2 × 2 的区域集约成 1 个元素的处理，缩小空间大小。
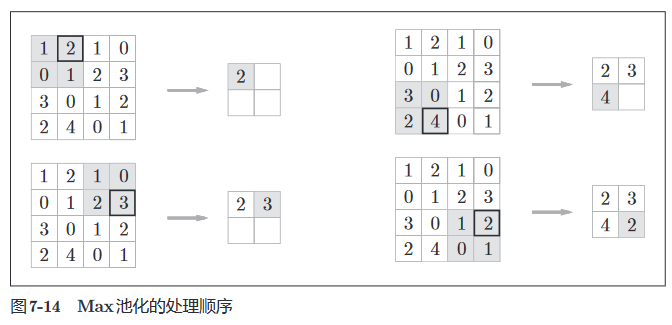
例子是按步幅2 进行2 × 2 的 Max 池化时的处理顺序。“Max 池化”是获取最大值的运算，“2 × 2”表示目标区域的大小。一般来说，池化的窗口大小会 和步幅设定成相同的值。
池化对于微小变化具有鲁棒性——输入数据发生微小偏差时，池化仍会反应相同的结果。
网络实现
卷积
我们并不采用多层for语句进行卷积运算，而是使用im2col函数。其能将输入图应用滤波器的部分展开成一列，如下。
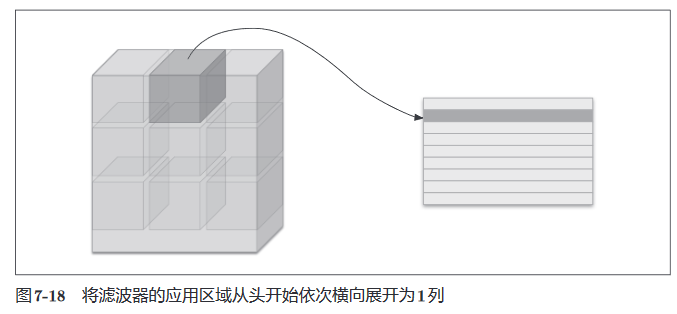
再将每个滤波器展开成一列，卷积运算便转化为了矩阵乘法，可以大大加快计算速度。
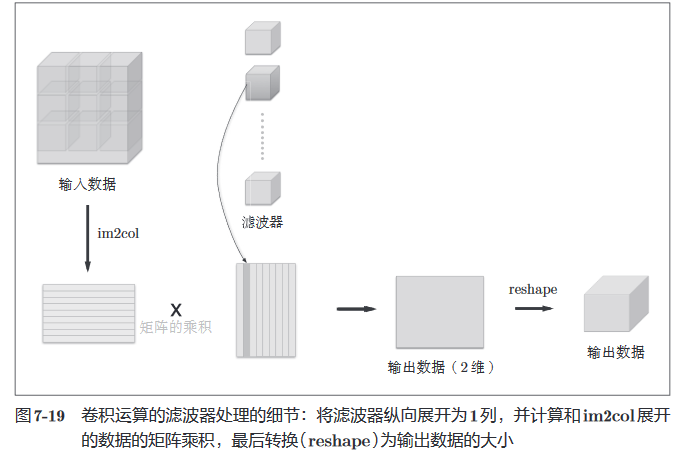
通过im2col展开，卷积层可以类似Affine层计算forward。而计算backward时，需要用到im2col的逆处理，即col2im函数，其余与Affine层的反向传播类似。
池化
在池化层中，使用im2col将应用于池化的区域展开，如下。
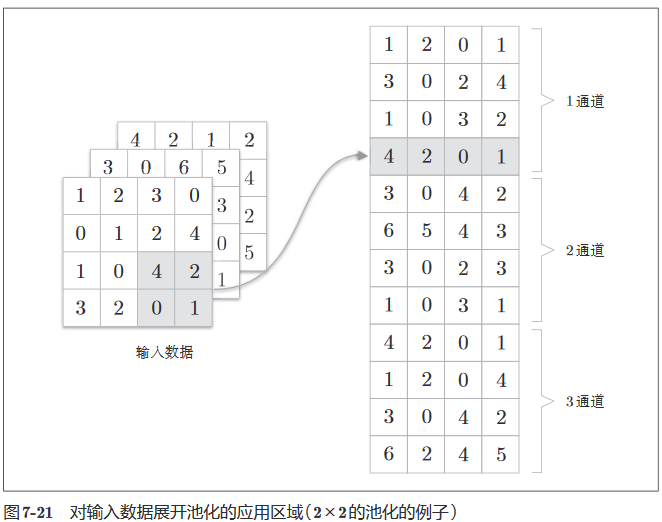
对应的池化操作即对矩阵的每行求最大值，再将形状变回对应维度即可，如下所示。
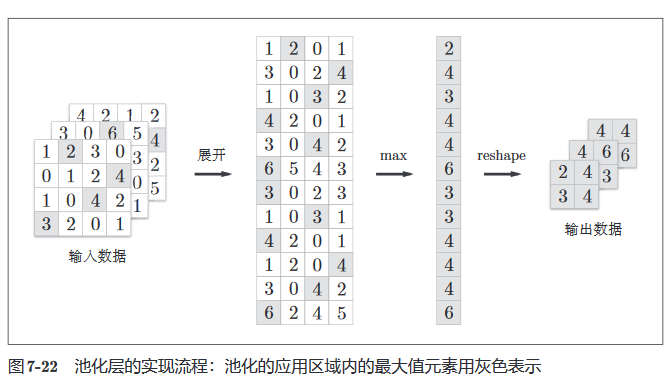
池化层的反向传播可以参考ReLu的max函数处理。
CNN的学习
简而言之，随着网络层次的不断加深，滤波器所提取的信息也越来越抽象。比如滤波器能逐渐识别边缘->纹理->物体部件->整体。具体可以参考如下的文献。
Matthew D. Zeiler and Rob Fergus（2014）: Visualizing and Understanding Convolutional Networks. In David Fleet, Tomas Pajdla, Bernt Schiele, & Tinne Tuytelaars, eds. Computer Vision – ECCV 2014. Lecture Notes in Computer Science. Springer International Publishing, 818 – 833.
A. Mahendran and A. Vedaldi（2015）: Understanding deep image representations by inverting them. In 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). 5188 – 5196.
代表性的CNN
LeNet
Y. Lecun, L. Bottou, Y. Bengio, and P. Haffner（1998）: Gradient-based learning applied to document recognition. Proceedings of the IEEE 86, 11 (November 1998), 2278 – 2324.
AlexNet
Alex Krizhevsky, Ilya Sutskever, and Geoffrey E. Hinton（2012）: ImageNet Classification with Deep Convolutional Neural Networks. In F. Pereira, C. J. C. Burges, L. Bottou, & K. Q. Weinberger, eds. Advances in Neural Information Processing Systems 25. Curran Associates, Inc., 1097 – 1105.